This is a very important topic to understand for the final exam. You will most likely be asked questions directly about it. You will also need to understand the exponential topic in order to understand the logarithm topic, which you will also most likely be asked about. This topic appears in other topics too. The most common examples are financial maths and calculus. Often it will also be one piece of solving a larger general algebra question. Not understanding the exponential will not just cost you marks in this topic, but will likely cost you marks in all the ones mentioned above.
An exponential means a number multiplied by itself a certain number of times. It is written as \(x^y\), which would mean \(x\) multiplied by itself \(y\) times.
To give a concrete example, \(2^3\) is \(2\) multiplied by itself \(3\) times, i.e. \(2 \times 2 \times 2\). So \(2^3=8\) because \(2 \times 2 \times 2 = 8\).
\(4^2=4 \times 4\), which is \(16\).
In the example \(x^y\) we call \(x\) the base and \(y\) the power or exponent or index. We will use power from now on.
What is \(a^{4}\) ?
What is \(w \times w \times w \times w\) ?
In the graph below you will see \(y=2^x\).
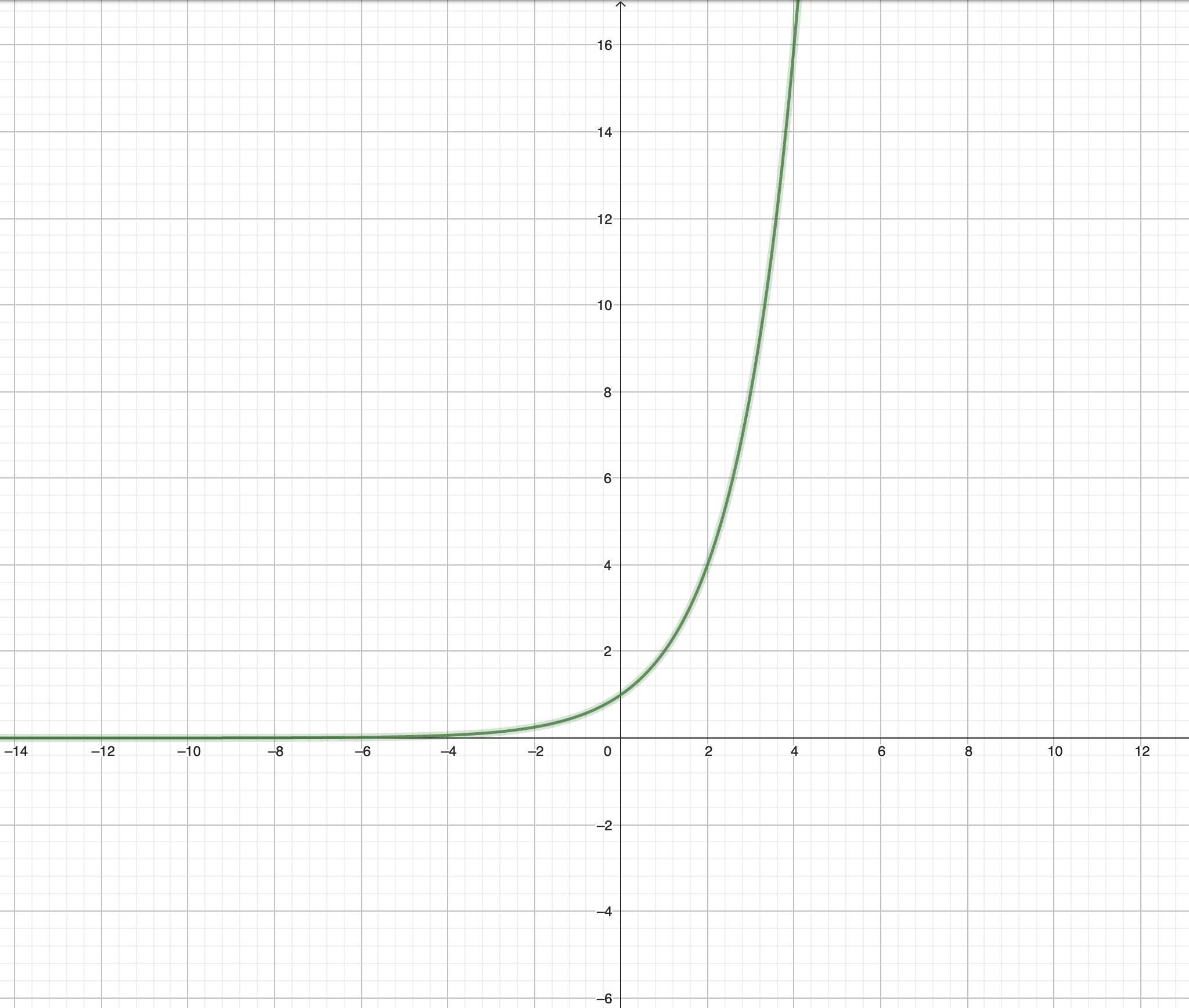
Note how when \(x=1\) then \(y=2\), in other words the curve passes through the point \((1,2)\). Note \(2^1\) means a product (series of multiplications) made by one single \(2\). This is just \(2\). Picture just a single \(2\) on its own.
Now what happens as \(x\) increases by \(1\)? \(y\) doubles. Because \(2^x\) means “x number of 2s multiplied together” everytime you increase \(x\) by \(1\), you are multiplying by yet another \(2\).
If instead of \(y=2^x\) we had \(y=3^x\) then \(y\) would triple every time \(x\) went up by \(1\) because we would now be doing another multiplication by \(3\) to the previous value.
In your exam log booklet there are a few rules about exponentials. You will work faster and be able to solve more difficult questions if you do not need to refer back to this booklet over and over, looking for any rule that seems like it might fit the question. So we will go over them, and you will understand why they are true. Applying them to solve problems will come easily to you once their truth is understood.
What is \((q \times q \times q) \times (q \times q \times q \times q \times q)\) ?
When multiplying numbers together, the order of multiplication does not matter. For example, take: \(2 \times 2 \times 5\)
We can do the \(2 \times 2\) first, leaving \(4 \times 5=20\).
Or we can do the \(2 \times 5\) first, leaving \(2 \times 10=20\).
It does not matter.
And so, if we have \(a \times a \times a \times a \times a\) we can group these with brackets all day long, and it would make no difference, e.g. \((a \times a) \times (a \times a) \times a\) — Doesn’t change anything.
Consider the most extreme case, where we try to use as many brackets as possible. In this case we would be bracketing every single \(a\) in the expression, and we’d be right back to multiplying them all one by one, as if the brackets were not there.
What is \((w \times w \times w \times w \times w) \times (w \times w \times w \times w \times w)\) ?
What is \(p^{3} \times p^{5}\) ?
What is \(n^{5} \times n^{4}\) ?
So when we have to deal with a product (multiplication) of exponentials that have the same base, we can expand each one out in its multiplication form. We then have one chain of multiplication being multiplied by another change of multiplication. We then stop pretending that these are two separate chains and treat them as one long chain of multiplications.
And you know how to express, as an exponential, a long chain of a number being multiplied by itself.
What is \(p^{c} \times p^{l}\) ?
So when we multiply exponentials with the same base, we get an exponential with the same base and the power of this new exponential is the sum of the originals.
Rule 1: \(a^b \times a^c = a^{b+c}\)
The base of an exponential can itself be an exponential. \({(x^y)}^z\) is an example of an exponential with power \(z\) and base \(x^y\).
Let’s simplify that. As in Rule 1 we can build an intuition about this by expanding out the expression.
What is \((z^{m})^{4}\) ?
You know from Rule 1 that multiplying exponentials with the same base creates a new exponential with a power that is the sum of the original powers.
What is \(x^{a} \times x^{k}\) ?
This means that \(x^y \times x^y \times x^y = x^{y+y+y}\)
And repeated addition of a number is equivalent to one multiplication.
Simplify \(y+y+y+y\)
Here is another way of looking at it. Expand \({(x^2)}^3\) all the way. First we expand the inner exponential \(x^2\) to get \((x \times x)^3\)
What is \(s^{5}\) ?
We now have an exponential of a product. Let’s expand this exponential in the same manner: \((x \times x) \times (x \times x) \times (x \times x)\)
We have repeated the original (inner) product 3 times because the outer exponential had a power of 3.
Recall that the brackets dividing a long product (aka multiplication) into different sections is actually meaningless.
What is \((q \times q \times q) \times (q \times q \times q \times q \times q)\) ?
So we expanded the inner exponential leading to a chain of \(x\) that was \(2\) long. We then expanded the outer exponential which repeated that chain \(3\) times. Leading to a total chain length of \(6\).
Now we can gather that chain back up into a single exponential.
What is \(d \times d \times d \times d\) ?
Try it yourself.
What is \((y^{4})^{4}\) ?
And more generally, the rule is:
What is \((s^{b})^{c}\) ?
Rule 2: \({(a^b)}^c = a^{b \times c}\)
You have already seen how multiplying exponentials with the same base results in an exponential with the same base, but the power of the new exponential is the sum of the powers of the original exponentials.
What is \(x^{a} \times x^{k}\) ?
Since we have \(a^b \times a^c=a^{b+c}\), consider what happens if we divide both sides by \(a^c\).
\(\frac{a^b \times a^c}{a^c} = \frac{a^{b+c}}{a^c}\)
We can simplify this a bit.
Simplify \(\frac{b \times z}{t \times z}\)
In general dividing by a value undoes the result of multiplying by that value. So if multiplying by an exponential results in that exponetial’s power being added, then dividing by the exponential should have the opposite result.
But let’s build an intuition about why. You have already shown that common factors in a fraction can be removed, it’s as simple as that.
Take \(\frac{x^4}{x^2}\), and expand it by expanding the top and bottom.
What is \(s^{5}\) ?
So we have \(\frac{x \times x \times x \times x}{x \times x}\) and we remove the common factors to get \(\frac{x \times x}{1}=x \times x\).
We can then convert this back to an exponential.
What is \(s \times s \times s \times s \times s\) ?
In general if we have a value (e.g. \(x\)) being multiplied in a chain \(N\) times on top of a fraction. And we have a chain of \(x\) being multiplied by \(K\) times on the bottom. And we remove the common \(x\)s from the top and bottom, how many are left on top (assuming the top had more to begin with)? \(N-K\)
With this all in mind let’s try it out.
What is \(\frac{x^{a}}{x^{n}}\) ?
The powers can be subtracted when dividing exponentials with the same base.
Rule 3: \(\frac{x^y}{x^z}=x^{y-z}\)
Sometimes you will have an exponential with a negative power, e.g. \(x^{-3}\), which you would prefer to deal with in terms of an exponential with a positive power. This transformation follows pretty simply from the previous Rule 3.
What is \(\frac{c}{p}\) ?
You can split any fraction into a multiplication, e.g. \(\frac{2}{3} = 2 \times \frac{1}{3}\).
It makes no difference whether the terms in the fraction are simple numbers, as in the above example, or something more complex like an exponential.
What is \(\frac{n^{c}}{n^{s}}\) ?
You know from Rule 4 that dividing an exponential by another exponential with the same base results in a subtraction of powers, i.e. \(\frac{x^n}{x^k} = x^{n-k}\)
You now can see that \(\frac{x^n}{x^k} = x^n \times \frac{1}{x^k} = x^{n-k}\)
You know that multiplying exponentials with the same base results in an addition of the powers, i.e. \(x^n \times x^k =x^{n+k}\).
In the case of \(x^n \times \frac{1}{x^k} = x^{n-k}\), the exponential \(x^n\) is being multiplied by something with the result being \(x^{n-k}\). Consider, what is this “something” ?
What is \(\frac{1}{k^{m}}\) ?
Looking at it another way, we can go back to \(x^n \times \frac{1}{x^k} = x^{n-k}\)
If we divide both sides by \(x^n\) it is removed from the left hand side, and we get \(\frac{1}{x^k} = \frac{x^{n-k}}{x^n}\)
What is \(\frac{c^{p}}{c^{z}}\) ?
You know that dividing exponentials with the same base results in subtracting the powers, so \(\frac{x^{n-k}}{x^n} = x^{n-k-n}\) , and needless to say, \(n-n=0\)
What is equivalent to \(o^{-c}\) ?
Rule 4: \(x^{-k} = \frac{1}{x^k}\)
Exponentials with fraction powers, i.e. \(x^{\frac{1}{2}}\) are one way of expressing a pretty common idea.
Suppose that we took that exponential and squared it, i.e. put it inside another exponential with a power of 2, we would have \({(x^{\frac{1}{2}})}^2\)
What is \((s^{b})^{c}\) ?
As you know from Rule 2. We can multiply the powers when we have an exponential inside an exponential, so \({(x^{\frac{1}{2}})}^2\) becomes \(x^{\frac{1}{2} \times 2}\).
What is \(\frac{t}{q}\) ?
As you saw in Rule 3. We can split a fraction into a product and vice versa, so let’s use that here: \(x^{\frac{1}{2} \times 2}\) becomes \(x^{\frac{2}{2}} = x^1 = x\).
And so in \({(x^{\frac{1}{2}})}^2\) the \(2\) and the \(\frac{1}{2}\) have undone each other.
How is the square root of \(n\) usually written ?
If \(\sqrt[]{x} = q\) what is \(q^{2}\) ?
As you can see, both \({(\sqrt{x})}^2 = x\) and \({(x^{\frac{1}{2}})}^2 = x\). We can conclude that \({(\sqrt{x})}^2 = {(x^{\frac{1}{2}})}^2\)
But we can generalise it. You know that \(\sqrt{x}\) means the square root of \(x\), which means the number that when squared gives \(x\). However, this is just a shorter way of writing it because we use the square root so often, but there is a more verbose way of writing that root.
How is the square root of \(b\) sometimes written ?
With \(\sqrt[2]{x}\) we are being explicit that this is a square root, which the \(2\) makes clear. As mentioned, this is the most commonly used root so the \(2\) is sometimes not included and just assumed to be there.
But what if we wanted the number that, when cubed (not squared), equals \(x\) ? How would we write that number?
How is the cubic root of \(m\) usually written ?
And so \({\sqrt[3]{x}}^3 = x\), but also \({(x^{\frac{1}{3}})}^3 = x\) for the reasons mentioned at the start of this rule.
If \(\sqrt[k]{x} = n\) what is \(n^{k}\) ?
What is \(y^{\frac{1}{m}}\) ?
And so we can see that an exponential with a fraction power is another way of writing a root. \(x^{\frac{1}{y}}\) is the same as \(\sqrt[y]{x}\), which signifies “the number that when raised to the power of \(y\) results in \(y\)”.
Rule 5: \(x^{\frac{1}{y}} = \sqrt[y]{x}\)
It may be that you have an exponential of a product and would prefer to deal with exponentials of the individual values in that product.
First let’s clarify what is a product, it is simply a multiplication. It can be \(x \times y\), it can be \(a \times b \times b\), etc. any series of values multiplied together is a product. And sometimes we have to deal with exponentials where the base is a product, e.g. \({(a \times b)}^3\).
Let’s do our usual trick of expanding this out.
What is equivalent to \((b \times o)^{6}\) ?
As we have by now established, the order of multiplication does not matter in a product. We can arrange the values any way we want.
What is equivalent to \((u \times x) \times (u \times x) \times (u \times x)\) ?
Now we have turned \({(a \times b)}^3\) into \(a \times a \times a \times b \times b \times b\). Although adding any brackets within this makes no difference, it can be useful for us to visualise the two groupings present.
What is equivalent to \(n \times n \times n \times n \times z \times z \times z \times z \times z\) ?
Now that we have \((a \times a \times a) \times (b \times b \times b)\) as usual we can group them back into exponentials.
What is equivalent to \((t \times t \times t \times t) \times (f \times f \times f \times f \times f)\) ?
Now let’s take an example of the rule from start to end:
What is equivalent to \((k \times w)^{2}\) ?
And finally the rule in the abstract:
What is equivalent to \((a \times g)^{v}\) ?
Rule 6: \({(a \times b)}^c = a^c \times b^c\)
For more help towards a high grade in Leaving Cert Maths, join Numereum now.